欢迎大家赞助一杯啤酒🍺 我们准备了下酒菜:Formal mathematics/Isabelle/ML, Formal verification/Coq/ACL2, C++/F#/Lisp
微积分
来自开放百科 - 灰狐
(版本间的差异)
小 (→简介) |
小 (→项目) |
||
| 第30行: | 第30行: | ||
==项目== | ==项目== | ||
*[https://freefem.org/ FreeFEM] is a popular 2D and 3D partial differential equations (PDE) solver | *[https://freefem.org/ FreeFEM] is a popular 2D and 3D partial differential equations (PDE) solver | ||
| + | |||
| + | ==文档== | ||
| + | |||
| + | ==书籍== | ||
| + | *《普林斯顿微积分读本 (修订版)》 Adrian Banner | ||
| + | *《偏微分方程讲义(第3版)》 O.A.奥列尼克, 郭思旭译 | ||
==教育== | ==教育== | ||
2022年12月16日 (五) 10:24的版本
| |
您可以在Wikipedia上了解到此条目的英文信息 微积分 Thanks, Wikipedia. |
微积分
目录 |
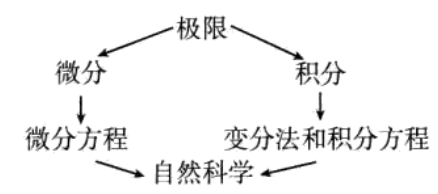
简介
微积分学也称微分积分学(拉丁语:Calculus),主要包括微分学和积分学两个部分,是研究极限、微分、积分和无穷级数等的一个数学分支。更本质的讲,微积分学是一门研究连续变化的学问。
历史
在数学著述的产量方面,柯西与欧拉相媲美,他撰写了大约800部专著和论文,几乎涉及了数学的所有分支。
他最伟大的贡献之一是他引入微积分的严密方法的三篇论文:
- 《工科大学分析讲义》(1821年)
- 《无穷小计算概要》(1823年)
- 《微分学讲义》(1829年)
通过这些著作,柯西在赋予他在微积分的特性方面比任何人的贡献都大,而这些特性一直保持至今。
摘自《微积分概念发展史》波耶,p276
概念
符号
应用
项目
- FreeFEM is a popular 2D and 3D partial differential equations (PDE) solver
文档
书籍
- 《普林斯顿微积分读本 (修订版)》 Adrian Banner
- 《偏微分方程讲义(第3版)》 O.A.奥列尼克, 郭思旭译
教育
图集
链接
分享您的观点