欢迎大家赞助一杯啤酒🍺 我们准备了下酒菜:Formal mathematics/Isabelle/ML, Formal verification/Coq/ACL2, C++/F#/Lisp
Mathematical analysis
来自开放百科 - 灰狐
(版本间的差异)
小 |
小 (→书籍) |
||
| (未显示1个用户的4个中间版本) | |||
| 第1行: | 第1行: | ||
{{SeeWikipedia}} | {{SeeWikipedia}} | ||
| − | 数学分析(mathematical | + | 数学分析(mathematical analysis) |
| + | |||
| + | ==简介== | ||
| + | 数学分析(mathematical analysis)区别于其他非数学类学生的高等数学内容,是分析学中最古老、最基本的分支,一般指以[[微积分]]学、无穷级数和解析函数等的一般理论为主要内容,并包括它们的理论基础(实数、函数、测度和极限的基本理论)的一个较为完整的数学学科。它也是大学数学专业的一门基础课程。 | ||
数学分析研究的内容包括实数、复数、实函数及复变函数。数学分析是由微积分演进而来,在微积分发展至现代阶段中,从应用中的方法总结升华为一类综合性分析方法,且初等微积分中也包括许多数学分析的基础概念及技巧,可以认为这些应用方法是高等微积分生成的前提。数学分析的方式和其几何有关,不过只要任一数学空间有定义邻域(拓扑空间)或是有针对两物件距离的定义(度量空间),就可以用数学分析的方式进行分析。 | 数学分析研究的内容包括实数、复数、实函数及复变函数。数学分析是由微积分演进而来,在微积分发展至现代阶段中,从应用中的方法总结升华为一类综合性分析方法,且初等微积分中也包括许多数学分析的基础概念及技巧,可以认为这些应用方法是高等微积分生成的前提。数学分析的方式和其几何有关,不过只要任一数学空间有定义邻域(拓扑空间)或是有针对两物件距离的定义(度量空间),就可以用数学分析的方式进行分析。 | ||
| + | |||
| + | [[文件:limit.png|极限]] | ||
| + | |||
| + | “自然界中的每一件事都满足最小或最大法则 。” | ||
| + | |||
| + | 欧拉在1743年发表的关于变分法的著作附录中写道。 | ||
==相关== | ==相关== | ||
| + | *[[微积分]] | ||
*[[Numerical analysis]] | *[[Numerical analysis]] | ||
*[[Computational mathematics]] | *[[Computational mathematics]] | ||
| + | |||
| + | ==项目== | ||
| + | |||
| + | ==文档== | ||
| + | |||
| + | ==书籍== | ||
| + | *《无穷分析引论(上、下)》 欧拉 | ||
| + | *《数学分析原理 第一卷 第9版)》 菲赫金哥尔茨,有1、2两卷 | ||
| + | *《数学分析 第一卷、第二卷 第7版》 《Mathematical Analysis I》《Mathematical Analysis II》 B. A. Zorich (卓里奇) | ||
| + | |||
| + | ==图集== | ||
==链接== | ==链接== | ||
[[category:mathematics]] | [[category:mathematics]] | ||
2022年10月28日 (五) 08:13的最后版本
| |
您可以在Wikipedia上了解到此条目的英文信息 Mathematical analysis Thanks, Wikipedia. |
数学分析(mathematical analysis)
目录 |
[编辑] 简介
数学分析(mathematical analysis)区别于其他非数学类学生的高等数学内容,是分析学中最古老、最基本的分支,一般指以微积分学、无穷级数和解析函数等的一般理论为主要内容,并包括它们的理论基础(实数、函数、测度和极限的基本理论)的一个较为完整的数学学科。它也是大学数学专业的一门基础课程。
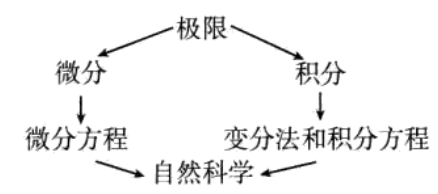
数学分析研究的内容包括实数、复数、实函数及复变函数。数学分析是由微积分演进而来,在微积分发展至现代阶段中,从应用中的方法总结升华为一类综合性分析方法,且初等微积分中也包括许多数学分析的基础概念及技巧,可以认为这些应用方法是高等微积分生成的前提。数学分析的方式和其几何有关,不过只要任一数学空间有定义邻域(拓扑空间)或是有针对两物件距离的定义(度量空间),就可以用数学分析的方式进行分析。
“自然界中的每一件事都满足最小或最大法则 。”
欧拉在1743年发表的关于变分法的著作附录中写道。
[编辑] 相关
[编辑] 项目
[编辑] 文档
[编辑] 书籍
- 《无穷分析引论(上、下)》 欧拉
- 《数学分析原理 第一卷 第9版)》 菲赫金哥尔茨,有1、2两卷
- 《数学分析 第一卷、第二卷 第7版》 《Mathematical Analysis I》《Mathematical Analysis II》 B. A. Zorich (卓里奇)
[编辑] 图集
[编辑] 链接
分享您的观点