欢迎大家赞助一杯啤酒🍺 我们准备了下酒菜：Formal mathematics/Isabelle/ML, Formal verification/Coq/ACL2, C++/F#/Lisp
Open Provable Foundation
来自开放百科 - 灰狐
（版本间的差异）
小 (→项目) |
小 (→项目) |
||
| 第18行： | 第18行： | ||
*[[Isabelle]] | *[[Isabelle]] | ||
*[[ACL2]] | *[[ACL2]] | ||
| + | *[[F*]] | ||
*[[Haskell]] [[Agda]] [[Idris]] 具有“证明即程序、命题为类型”的特征。 | *[[Haskell]] [[Agda]] [[Idris]] 具有“证明即程序、命题为类型”的特征。 | ||
*[https://github.com/seL4/l4v seL4] The world's most highly assured OS kernel, specification and proofs with isabelle. [https://github.com/seL4/l4v/tree/master/spec/haskell The seL4 Haskell Model] [[Haskell]] | *[https://github.com/seL4/l4v seL4] The world's most highly assured OS kernel, specification and proofs with isabelle. [https://github.com/seL4/l4v/tree/master/spec/haskell The seL4 Haskell Model] [[Haskell]] | ||
2022年2月6日 (日) 13:49的版本
Open Provable Foundation
目录 |
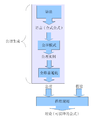
简介
理论
- 数学和逻辑
- 数理逻辑
- 证明论（元数学）
- 分析哲学
- 形式科学是指主要研究对象为抽象形态的科学，如逻辑、数学、数理逻辑、信息论、统计学（数理统计学）、理论计算机科学（计算理论）、经济学（博弈论）等。
项目
- Provably Awesome
- proof assistant
- Coq
- Isabelle
- ACL2
- F*
- Haskell Agda Idris 具有“证明即程序、命题为类型”的特征。
- seL4 The world's most highly assured OS kernel, specification and proofs with isabelle. The seL4 Haskell Model Haskell
图集
希尔伯特演绎系统
认知科学
isabelle
isabelle插件
链接
分享您的观点
