ACL2

2024年12月4日 (三) 03:53的最后版本

您可以在Wikipedia上了解到此条目的英文信息 ACL2 Thanks, Wikipedia.

ACL2

[编辑] 简介

ACL2 Theorem Prover

ACL2（A Computational Logic for Applicative Common Lisp，用于通用Lisp的计算逻辑）是由一个程序语言、一套一阶逻辑的可拓理论、以及一个机械化的定理证明器所组成的软件系统。ACL2 从设计上支持基于归纳逻辑理论的自动推理，可应用于软件或硬件系统的验证。ACL2 使用 Common Lisp。ACL2 采用 BSD三条款许可证，3-clause BSD 与 GNU GPL 兼容。

ACL2 程序语言可看作是一个函数式（无任何副作用）的 Common Lisp 变体

[编辑] 功能

• ALC2 type-related concepts

[编辑] 指南

A Brief ACL2 Tutorial

Debian

$ sudo apt install acl2
$ acl2
GCL (GNU Common Lisp) ...
ACL2>(@ acl2-version)
"ACL2 Version 8.4"
ACL2 !>:doc max

• Hyper-Card for ACL2 Programming

函数定义

• defun
• defunc  ;; with contracts
• defunec ;; with contracts extending

[编辑] 编程语言

• ACL2 programming language
• Yul 编程语言被用作编译以 Solidity 语言编写的Ethereum 智能合约的中间语言。然而，Yul 被设计成比 Solidity 更通用，并可能很快找到更多的应用。
• Imp 是一种简单的编程语言，主要用于教学目的。
• Java An ACL2 library for Java

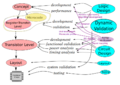
[编辑] 形式化验证

• Introduction-to-the-theorem-prover
• Hardware-verification
• Software-verification
• Proof-automation
• Automated Program Transformations (APT) 建立在ACL2定理验证器上，可以高度自动化地转换程序和程序规范，所有由APT生成的证明都由定理验证器检查。
• SOFT（二阶函数和定理）是一个模仿ACL2一阶逻辑中的二阶函数和定理的工具。
• Zcash 是一种区块链加密货币，通过零知识证明（zero-knowledge proofs）提供保密性。
• Bitcoin 库包含比特币某些方面的形式化模型
• ACL2 Ethereum Project
• Ethereum 库包含以太坊某些方面的形式化模型
• Milawa 是一个类似 ACL2 逻辑的 "自我验证 "定理检验器。
• Rp-rewriter (retain property 保留属性) 是一个经过验证的条款处理器，可以用来替代ACL2的改写器（rewriter）。对于某些情况，在构建公理时可以提供时间效率和便利。

[编辑] 并行计算

Parallel programming in ACL2(p)

[编辑] 项目

• ACL2 @ GitHub
• ACL2 Sedan theorem prover (ACL2s) with Eclipse IDE
• ipasir The Standard Interface for Incremental Satisfiability Solving（递增可满足性求解）
• Proof Pad is a web based IDE for ACL2, using a Kubernetes based backend.

[编辑] 文档

ACL2 有自己的一套文档、图书 出版系统，文档的源文件都是 .lisp 结尾, xdoc 包，defxdoc constructors（构造器）函数组成。

XDOC is a tool for documenting ACL2 books.

• Industrial Hardware and Software Verification with ACL2
• Industrial Use (of ACL2) for Hardware Verification

[编辑] 图书

Books and Papers

• 《A Computational Logic》
• 《Computer-Aided Reasoning: An Approach》
• 《Computer-Aided Reasoning: ACL2 Case Studies》
• 《Essential Logic for Computer Science》
• 《Scalable Techniques for Formal Verification》
• 《Design and Verification of Microprocessor Systems for High-Assurance Applications》
• 《Formal Verification of Floating-Point Hardware Design: A Mathematical Approach》

[编辑] STEM

• Recursion and Induction -- CS 389r Recursion and Induction

[编辑] 图集

• 

  ACL2系统架构

• 

  ACL2形式化验证设计流程

• 

  ACL2形式化验证流程

• 

  Proof Pad

[编辑] 链接

• ACL2官网
• ACL2文档
• Kestrel Institute
• Warren A. Hunt, Jr.
• Computational Logic Inc.(CLI)