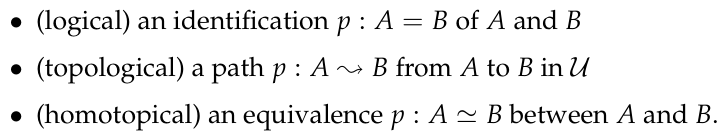Formal mathematics

您可以在Wikipedia上了解到此条目的英文信息 Formal mathematics Thanks, Wikipedia.

Formal mathematics 形式化数学

简介

What is Formal Math?

Open Provable Foundation

数理逻辑/数学证明

Formalized Mathematics

ML (Meta language -> Mathematics language) 很有寓意，ML 实力体现在编译器构建、自动化定理证明和形式化验证等。

理论

范畴论（Category theory）是数学的一门学科，以抽象的方法处理数学概念，将这些概念形式化成一组组的“对象”及“态射”，数学中许多重要的领域可以形式化为范畴。

类型论在绝大多数计算机证明辅助系统中被用作集合论的替代理论，因为集合论的语言难以转化成计算机辅助证明的形式语言。

HoTT Coq library homotopy type theory (HoTT) 同伦类型论是一个结合了几个不同领域的一个新的数学分支。
homotopy type theory (HoTT) and Cubical type theory
Hindley–Milner (HM) type system Classic Algorithm W for type inference.

同伦理论在2002年菲尔兹奖获得者符拉基米尔·弗沃特斯基（Vladimir Voevodsky GitHub账号）关于米尔诺猜想的工作中发挥了重要作用。弗沃特斯基（2017年9月30日因为动脉瘤于普林斯顿去世）近年来致力于使用一价语义构造新数学基础的理论体系 UniMath，使用证明辅助工具 Coq 实现。

The UniMath project was started in 2014 by merging the repository Foundations, by Vladimir Voevodsky (written in 2010)

分开记忆：同构（iso - morphism）同态（homo - morphism）同伦（homo - topy）同胚（homeo - morphism）同调（homo - logy）同痕（iso - topy）

助记:homo - 表示基本相同但不全同；iso - 表示全同；morphism - 表示映射。同胚是拓扑空间范畴中的同构，同痕是同伦的加细版。

不对等性公理（univalence axiom）确定了以下三个概念

形式语言

在数学、逻辑和计算机科学中，形式语言是用精确的数学或机器可处理的公式定义的语言。

代数语言学又称做形式语言学，主要研究如何对语言的形式结构进行严格的数学描述，并据此创立形式化的普遍语法。

项目

Coq Univalent Mathematics
Agda Univalent mathematics in Agda
ACL2
Isabelle
Prolog logic programming language
OCaml Zarith library 对任意精度（arbitrary-precision）的整数进行算术和逻辑运算
Lean mathlib Lean
IsarMathLib Proofs by humans, for humans, formally verified by Isabelle/ZF proof assistant
lean-gym Lean
Calculating Programs
Charity is a categorical programming language
Groupoid Infinity Institute 研究所正在做数学的形式化，其形式化编程语言称为 Anders 1.3.0，是立方体类型系统（cubical type systems）的 CCHM/HTS 变体（variant ）Groupoid @ GitHub
Henk: Pure Type System 是带有通用量词（universal quantifier）和宇宙无穷数量（infinity number of universes）的最小语言，用于一致的类型检查和规范化（consistent typechecking and normalization） made by Erlang
Anders is a Modal HoTT proof assistant, written in OCaml and Pug.
Cubical Type Theory written in Haskell.