欢迎大家赞助一杯啤酒🍺 我们准备了下酒菜：Formal mathematics/Isabelle/ML, Formal verification/Coq/ACL2, C++/F#/Lisp
Open Provable Foundation
来自开放百科 - 灰狐
（版本间的差异）
小 (→SAT) |
小 (→简介) |
||
| （未显示1个用户的5个中间版本） | |||
| 第6行： | 第6行： | ||
*[[Formal verification]] | *[[Formal verification]] | ||
*[https://fm.mizar.org/ Formalized Mathematics] | *[https://fm.mizar.org/ Formalized Mathematics] | ||
| + | *[[Formal mathematics]] | ||
| + | |||
| + | Proof Assistant Foundations | ||
| + | *[[Coq]] | ||
| + | *[[Agda]] | ||
| + | *[[Lean]] | ||
| + | *[[Isabelle]]/HOL | ||
==理论== | ==理论== | ||
| 第40行： | 第47行： | ||
==项目== | ==项目== | ||
| + | [[文件:nasa-fm-logo.jpg|right|NASA Langley's Formal Methods]] | ||
[[文件:Agda-language-logo.png|right|Agda]] | [[文件:Agda-language-logo.png|right|Agda]] | ||
[[文件:Coq-logo.png|right|Coq]] | [[文件:Coq-logo.png|right|Coq]] | ||
[[文件:Isabelle-logo.gif|right|isabelle]] | [[文件:Isabelle-logo.gif|right|isabelle]] | ||
| − | |||
[[文件:FMCAD-logo.png|right|FMCAD]] | [[文件:FMCAD-logo.png|right|FMCAD]] | ||
*[https://github.com/awesomo4000/awesome-provable Provably Awesome] [[文件:awesome.png]] | *[https://github.com/awesomo4000/awesome-provable Provably Awesome] [[文件:awesome.png]] | ||
| 第65行： | 第72行： | ||
*[https://www.gnu.org/software/c-graph GNU C-Graph] Convolution Theorem Visualization（卷积定理的可视化） [[文件:gnu.tiny.png]] | *[https://www.gnu.org/software/c-graph GNU C-Graph] Convolution Theorem Visualization（卷积定理的可视化） [[文件:gnu.tiny.png]] | ||
*[https://dezyne.org/ Dezyne] 是一种编程语言和一套工具集，用于指定、验证、核实、模拟、记录和实现嵌入式和网络物理系统的并发控制软件。 | *[https://dezyne.org/ Dezyne] 是一种编程语言和一套工具集，用于指定、验证、核实、模拟、记录和实现嵌入式和网络物理系统的并发控制软件。 | ||
| + | |||
| + | ==图书== | ||
| + | *[https://www.nuprl.org/book/ 《Implementing Mathematics with The Nuprl Proof Development System》] | ||
| + | *[https://homotopytypetheory.org/book/ 《Homotopy Type Theory: Univalent Foundations of Mathematics》] The Univalent Foundations Program | ||
| + | [[coq|更多图书>>>]] | ||
==图集== | ==图集== | ||
| 第84行： | 第96行： | ||
[[category:formal]] | [[category:formal]] | ||
| + | [[category:proof assistant]] | ||
| + | [[category:reasoning]] | ||
| + | [[category:mathematics]] | ||
[[category:ML]] | [[category:ML]] | ||
| + | [[category:coq]] | ||
[[category:OCaml]] | [[category:OCaml]] | ||
[[category:haskell]] | [[category:haskell]] | ||
[[category:HDL]] | [[category:HDL]] | ||
[[category:Huihoo Foundation]] | [[category:Huihoo Foundation]] | ||
2023年8月4日 (五) 08:59的最后版本
Open Provable Foundation
目录 |
[编辑] 简介
Open Provable Foundation（开放可证明基础）
Proof Assistant Foundations
[编辑] 理论
- 数学和逻辑
- 数理逻辑
- 证明论（元数学）
- 分析哲学
- 形式科学是指主要研究对象为抽象形态的科学，如逻辑、数学、数理逻辑、信息论、统计学（数理统计学）、理论计算机科学（计算理论）、经济学（博弈论）等。
[编辑] SMT
可满足性模理论的基本思想是针对多种数据类型和相应的谓词逻辑理论，提出一个一般的框架，使得可以求解特定背景理论下的谓词逻辑公式的可满足性判定问题，进一步，可以求解涵盖多种理论的混合逻辑公式的可满足性判定问题。可满足性模理论与交互式定理证明相比，能够处理的逻辑公式要少一些，一般考虑无量词或者量词嵌套较少的谓词逻辑公式，但其优势在于能够实现逻辑推理的完全自动化。可满足性模理论考虑的谓词逻辑理论主要包括含有等于符号的未解释函数（EUF）、位向量（BV）、数组（Array）、整数线性算术（LIA）、实数线性算术（LRA）、整数非线性算术（NIA）、字符串（String）等。求解SMT公式可满足性问题的工具被称为SMT求解器。目前，比较有代表性的SMT求解器有微软开发的Z3求解器、美国斯坦福大学和爱荷华大学开发的CVC4/CVC5求解器、美国斯坦福国际研究院开发的Yices求解器等。对SMT求解的研究不但是自动推理、约束求解领域主流国际会议IJCAR/CADE、CP和SAT的主题，同时也是形式验证和编程语言领域的重要国际会议CAV、POPL、FM、TACAS上非常活跃的议题。SMT同时也受到产业界的高度关注，微软、英特尔、亚马逊、Cadence等公司的研究院或实验室都在开展与SMT相关的研究项目。
- Satisfiability Modulo Theories (SMT) 可满足性模理论指函数和关系符号在背景理论中进行解释的谓词逻辑公式的可满足性判定问题，SMT求解器已经成为软件工程、编程语言、信息安全领域的基础引擎。
- SMT研讨会（SMT Workshop）
- SMT-LIB
- International Satisfiability Modulo Theories Competition (SMT-COMP) 国际可满足性模理论竞赛
- SMT @ Microsoft SMT在微软很火
- SMT Slides
- Software Verification with Satisfiability Modulo Theories（一） （二）
- Satisfiability with and without theories
- Satisfiability Modulo Theories (SMT): Ideas and Applications, Universita Degli Studi di Milano, Italy, March 2010 (part 1 part 2 part 3 part 4 assignment).
[编辑] SAT
Boolean Satisfiability Problem（SAT）布尔可满足性问题
[编辑] Emacs
[编辑] 项目
- Provably Awesome
- ML 语言家族适用于形式语言、计算机辅助定理证明、证明助理、逻辑语言、一阶逻辑、论证软件、代码验证等形式化领域。
- Z3
- Agda is a dependently typed programming language / interactive theorem prover.
- Alt-Ergo An SMT Solver For Software Verification
- OpenSMT
- CVC5 CVC4 CVC3
- Haskell, Agda, Idris, Liquid Haskell 具有“证明即程序、命题为类型”的特征。
- F*
- ACL2
- proof assistant
- Coq
- Isabelle
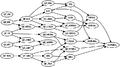
- HOL = functional programming + logic HOL Interactive Theorem Prover 文档 HOL Theory Hierarchy (Theory Graph)
- seL4 The world's most highly assured OS kernel, specification and proofs with isabelle. The seL4 Haskell Model Haskell
- Trustworthy Systems Formal methods
- Hardware description language for Formal verification
- NASA Langley Formal Methods Research Program
- GNU C-Graph Convolution Theorem Visualization（卷积定理的可视化）
- Dezyne 是一种编程语言和一套工具集，用于指定、验证、核实、模拟、记录和实现嵌入式和网络物理系统的并发控制软件。
[编辑] 图书
- 《Implementing Mathematics with The Nuprl Proof Development System》
- 《Homotopy Type Theory: Univalent Foundations of Mathematics》 The Univalent Foundations Program
[编辑] 图集
PVS架构
SMT-LIB logics
希尔伯特演绎系统
认知科学
isabelle
isabelle插件
CakeML
Triton
ATP Process
[编辑] 链接
分享您的观点
