Formal verification

来自开放百科 - 灰狐
（版本间的差异）
跳转到： 导航, 搜索
小 (→‎链接)
小 (→‎机器证明)
第21行： 第21行：
  
 
笛卡尔曾有过一个宏伟的设想：”一切问题化为数学问题，一切数学问题化为代数问题，一切代数问题化为代数方程求解问题。“他把问题问题想得过于简单了。如果他的设想真能实现，那就不仅是数学的机械化，而且是全部科学的机械化。因为，代数求解是可以机械化的。但笛卡尔没有停留在空想，他所创立的解析几何，在空间形式和数量关系之间架起了一座划时代的桥梁，实现了初等几何问题代数化。这为后来的几何定理机器证明的代数方法打下了基础。p.21
 
笛卡尔曾有过一个宏伟的设想：”一切问题化为数学问题，一切数学问题化为代数问题，一切代数问题化为代数方程求解问题。“他把问题问题想得过于简单了。如果他的设想真能实现，那就不仅是数学的机械化，而且是全部科学的机械化。因为，代数求解是可以机械化的。但笛卡尔没有停留在空想，他所创立的解析几何，在空间形式和数量关系之间架起了一座划时代的桥梁，实现了初等几何问题代数化。这为后来的几何定理机器证明的代数方法打下了基础。p.21
 +
 +
1977年，吴文俊提出的定理机器证明新方法正式发表。使用这新方法（简称吴法），可以在微机上迅速地证明很不简单的几何定理，如西姆松定理、费尔哈定理、莫勒定理等等；还能发现新的不平凡的的几何定理。1989年，访美学者周咸青基于吴法编制的 Lisp 程序（所谓”证明器“）在计算机上证明了512条定理。这些定理大多是不平凡的，其中还有新定理。证明每条定理所用的机器实践一般才几秒钟。p.27-28
  
 
《王者之路 机器证明及其应用》吴文俊等
 
《王者之路 机器证明及其应用》吴文俊等

2022年8月14日 (日) 06:18的版本

Wikipedia-35x35.png 您可以在Wikipedia上了解到此条目的英文信息 Formal verification Thanks, Wikipedia.

Formal verification

目录

简介

“在科学的问题上，一千人的权威比不上一个人谦卑的推理。” ——伽利略

Open Provable Foundation

Formal verification, Proof assistant, Theorem Prover, Software verification, Hardware verification ...

形式验证的含义是根据某个或某些形式规范或属性，使用数学的方法证明其正确性或非正确性。

形式验证可以分为三大类：抽象解释（Abstract Interpretation）、形式模型检查（Formal Model Checking，也被称作特性检查）和定理证明（Theory Prover）。

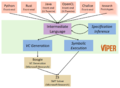
自动化定理证明（Automated theorem proving，ATP）目前是自动推理（Automated reasoning，AR）体系中发展最好的部分，它的目的是为使用电子计算机程序来进行数学定理的证明。对于不同的公理系统，它能够推论出一个定理在此系统下是正确的，还是不可证明的，或者错误的。

这里指包含 Proof assistant 证明助理（证明助手） 在内的所有形式化相关主题，包含计算机辅助定理证明、Coq 证明助理、函数式编程、操作语义、用于论证软件的逻辑和技术、静态类型系统、基于性质的随机测试、以及对实践中编程代码的验证等。

机器证明

笛卡尔曾有过一个宏伟的设想：”一切问题化为数学问题，一切数学问题化为代数问题，一切代数问题化为代数方程求解问题。“他把问题问题想得过于简单了。如果他的设想真能实现，那就不仅是数学的机械化，而且是全部科学的机械化。因为，代数求解是可以机械化的。但笛卡尔没有停留在空想，他所创立的解析几何，在空间形式和数量关系之间架起了一座划时代的桥梁，实现了初等几何问题代数化。这为后来的几何定理机器证明的代数方法打下了基础。p.21

1977年，吴文俊提出的定理机器证明新方法正式发表。使用这新方法（简称吴法），可以在微机上迅速地证明很不简单的几何定理，如西姆松定理、费尔哈定理、莫勒定理等等；还能发现新的不平凡的的几何定理。1989年，访美学者周咸青基于吴法编制的 Lisp 程序（所谓”证明器“）在计算机上证明了512条定理。这些定理大多是不平凡的，其中还有新定理。证明每条定理所用的机器实践一般才几秒钟。p.27-28

《王者之路 机器证明及其应用》吴文俊等

新闻

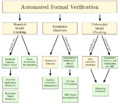
V & V

验证（Verification）与确认（Validation）

  • Verification 验证表明的是满足规定要求。
  • Validation 确认就是检查最终产品是否达到顾客使用要求。

参考

理论

Metamath

形式科学是指主要研究对象为抽象形态的科学，如逻辑、数学、数理逻辑、信息论、统计学（数理统计学）、理论计算机科学（计算理论）、经济学（博弈论）等。

Metamath 是用来发展严格形式化数学定义及证明的一款语言，亦指用来验证该语言的证明验证器，以及存有逻辑、集合论、数论、群论、代数、数学分析、拓扑学、希尔伯特空间及量子逻辑等领域中数万条已证明定理且仍不断在增加中的数据库。灰狐镜像

形式逻辑有传统与现代（即数理逻辑）之分，简单地说，形式逻辑是研究思维的形式及其规律的。

数理逻辑（Mathematical logic）是数学的一个分支，其研究对象是对证明和计算这两个直观概念进行符号化以后的形式系统。数理逻辑是数学基础的一个不可缺少的组成部分。

证明论（又名元数学）是数理逻辑的一个分支，它将数学证明表达为形式化的数学客体，从而通过数学技术来简化对他们的分析。证明通常用归纳式地定义的数据结构来表达，例如链表，盒链表，或者树，它们根据逻辑系统的公理和推理规则构造。因此，证明论本质上是语法逻辑，和本质上是语义学的模型论形相反。和模型论，公理化集合论，以及递归论一起，证明论被称为数学基础的四大支柱之一。

形式（formal）语言是人工语言（constructed）的一种，是从特定的初始符号出发经过特定的形成规则所形成的语言，比如电报代码、计算机语言、数学语言、逻辑语言等。

指南

在数学、逻辑和计算机科学中，形式语言（Formal language）是用精确的数学或机器可处理的公式定义的语言。

在计算机科学和数理逻辑中，证明助手或交互式定理检验器是一种软件工具，通过人机协作来协助开发形式证明。

在计算机科学和软件工程领域，形式化方法是使用适当的数学分析以提高设计的可靠性和强健性，适合于软件和硬件系统的描述、开发和验证。

形式验证（Formal verification）可以分为三大类：抽象解释（Abstract Interpretation）、形式模型检查（Formal Model Checking，也称作特性检查）和定理证明（Theory Prover）。

非形式化证明是算法，形式化证明是代码。

Formal-Verification.png DeepSpec The Science of Deep Specification

覆盖的核心概念有：

  • 逻辑学中的基本工具，用于准确地提出并论证关于程序的假设，逻辑学被称之为计算机科学的微积分；
  • 证明助理用于构造严谨的逻辑论据，分为两类：自动定理证明器和证明助理（如：Coq、Isabelle、Agda）；
  • 函数式编程思想，同时作为一种编程方法来简化程序的论证，以及架起程序和逻辑学之间的桥梁。

语言

Purely-functional-programming.png

项目

Coq
Z3
isabelle
Lean
ACL2
Deepspec-logo.png
Vellvm
KeY

STEM

研究组织

Automated Reasoning Group
NASA Langley's Formal Methods

文档

图书

  • 《Software Foundations》 软件基础系列是对可靠软件的数学基础的广泛介绍。该系列的主要创新之处在于，每一个细节都是百分之百的形式化和机器检查：每一卷的整个文本，包括练习，实际上是Coq证明助手的 "证明脚本"。
  • 《软件基础》系列广泛地介绍了可靠软件的数学基础，这是《Software Foundations》中文版。
  • 《芯片验证漫游指南：从系统理论到UVM的验证全视界》刘斌

数字集成系统的验证，是提高设计芯片一次流片成功的关键。随着芯片制造工艺的更加精细，芯片制造费用的不断增加，芯片功能越来越复杂，验证的重要性也日益增加。

图集

  • 证明助手

  • 规范

  • 验证

  • VST

  • CompCert

  • 希尔伯特演绎系统

  • isabelle

  • isabelle插件

  • isabelle实现

  • 认知科学

  • Viper

  • Nuprl5 FDL

  • F*

  • 真值表

  • 命题逻辑的符号

  • HOL家族

  • HOL4 Emacs

  • Automated Formal Verification

  • HiFrog

  • KeY架构

  • KeY & JML

  • KeY SED

  • VLSI设计形式化验证

链接

Runtime Verification
bluespec
来自“http://wiki.huihoo.com/wiki/?title=Formal_verification&oldid=165178”
分享您的观点
个人工具
名字空间

变换
操作
导航
工具箱