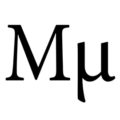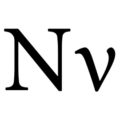Mathematics

来自开放百科 - 灰狐
（版本间的差异）
跳转到： 导航, 搜索
小 (→‎研究所)
小 (→‎简介)
 
（未显示1个用户的3个中间版本）
第15行： 第15行：
  
 
重要数学分支：代数几何、微分几何、拓扑空间（拓扑学）...
 
重要数学分支：代数几何、微分几何、拓扑空间（拓扑学）...
 +
 +
数学家研究的不是对象，而是对象之间的关系。
 +
对于他们来说，只要关系不变，就完全可以用另一组对象来取代现有的对象。
 +
他们不关注对象的内容，只关注形式。
 +
 +
——庞加莱《科学与假设》（Science and Hypothesis）
 +
 +
==计划纲领==
 +
爱尔兰根纲领（Erlangen program）：认为几何就是研究变换群下不变的性质，几何的不同实为不同的变换群所致
 +
 +
朗兰兹纲领（Langlands program）：述说数论与群论的深刻联系，被视为“数学的一种大统一理论”
 +
 +
希尔伯特计划（Hilbert's program）：主要目标是为全部的数学提供一个安全的理论基础
  
 
==数学分类数学百科==
 
==数学分类数学百科==
第55行： 第68行：
 
==分支领域==
 
==分支领域==
 
[[文件:drum-vibration-mode.gif|right|泛函分析（圆形鼓皮的理想化振动模式）]]
 
[[文件:drum-vibration-mode.gif|right|泛函分析（圆形鼓皮的理想化振动模式）]]
 +
*[[algebra|代数]]
 
*数论
 
*数论
 
*[[微积分]]
 
*[[微积分]]
第151行： 第165行：
 
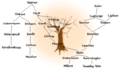
image:mathematics-genealogy-skeleton.png|数学谱系
 
image:mathematics-genealogy-skeleton.png|数学谱系
 
image:branch-of-mathematics.jpg|数学的各个分支
 
image:branch-of-mathematics.jpg|数学的各个分支
 +
image:The-Periodic-Table-of-Finite-Simple-Groups.jpg|有限简单群的周期表
 
image:mathematicians.png|数学家
 
image:mathematicians.png|数学家
 
image:Mathematical-Thought-from-Ancient-to-Modern-Times.jpg|古今数学思想
 
image:Mathematical-Thought-from-Ancient-to-Modern-Times.jpg|古今数学思想

2023年8月13日 (日) 23:20的最后版本

Wikipedia-35x35.png 您可以在Wikipedia上了解到此条目的英文信息 Mathematics Thanks, Wikipedia.

数学（Mathematics）

数学之美

Topology-01.gif
Topology-02.gif

目录

[编辑] 简介

数学，是一门研究数量、结构以及空间等概念及其变化的学科。

极限概念是数学的核心，分析的核心是微积分。

数学三大基石：分析、代数、几何

重要数学分支：代数几何、微分几何、拓扑空间（拓扑学）...

数学家研究的不是对象，而是对象之间的关系。 对于他们来说，只要关系不变，就完全可以用另一组对象来取代现有的对象。 他们不关注对象的内容，只关注形式。

——庞加莱《科学与假设》（Science and Hypothesis）

[编辑] 计划纲领

爱尔兰根纲领（Erlangen program）：认为几何就是研究变换群下不变的性质，几何的不同实为不同的变换群所致

朗兰兹纲领（Langlands program）：述说数论与群论的深刻联系，被视为“数学的一种大统一理论”

希尔伯特计划（Hilbert's program）：主要目标是为全部的数学提供一个安全的理论基础

[编辑] 数学分类数学百科

PlanetMath 是一本自由、协作的网络数学百科全书。强调同行评审、严密、公开、具教育性、实时内容、内容互连、以及群体协作，所有内容使用 LaTeX 编写，采用 CC 知识共享许可协议。

PlanetMath 的目标是成为一本综合性的网络数学百科全书，另一个主流是由 Wolfram Research 维护的 MathWorld

以同行评审为中心的性质使得 PlanetMath 的内容比起 MathWorld 更与众不同、更严密及更有学院味道。

PlanetMath 每一个条目都使用美国数学学会（AMS）的分类系统来分门别类。

数学学科分类标准（Mathematics Subject Classification，MSC）是由美国数学学会（American Mathematical Society，AMS）策划的建立在两个主要的引文数据库数学评论和数学文摘上的字母数字混合的分类方案。

[编辑] 方法论

数学哲学

费曼学习法

数学的思维方式是一种科学的思维方式，它是一个全过程：观察客观现象，提出要研究的问题，抓住主要特征，抽象出概念，或者建立模型；运用解剖麻雀、直觉、归纳、类比、联想、逻辑推理等进行探索，猜测可能有的规律；采用公理化的方法，即只使用公理、定义和已经证明了的定理进行逻辑推理来严密论证，揭示出事物的内在规律，从而使纷繁复杂的现象变得井然有序。”观察——抽象——探索——猜测——论证”是数学思维方式全过程的五个重要环节。按照数学的思维方式学习数学是学好数学的正确途径，在学习教学过程中受到教学思维方式的熏陶和训练，对于学生今后从事任何工作都有帮助，终身受益。《数学的思维方式与创新》（序言）

就像格罗滕迪克所说：“构成一个研究者创造力和想象力的本质，是他们聆听事情内部声音的能力。”这里没有等级高下，没有阶层之分，在对未知的探索前人人平等，每个人都拥有绝对的自由。每一个数学家愿意孜孜不倦研究数学的最主要动力不是别的，是我们享受那种日复一日，能够从现实生活中超越出来，去聆听，和发现世界运行规律的时刻。——许晨阳

[编辑] 数学素养

数学六大核心素养：

  • 数学抽象（mathematical abstraction）
  • 逻辑推理（logical reasoning）
  • 数学建模（mathematical modeling）
  • 直观想象（intuitive imagination）
  • 数学运算（mathematical operation）
  • 数据分析（data analysis）

[编辑] 数学物理

在数学的所有学科中，微分方程理论是最重要的。物理学的所有分支提出问题，它们可以被归结为微分方程的积分。更一般地，对于所有依赖于时间的自然现象由微分方程理论所给出。—— S.李 (1894)

泛函分析在数学物理方程，概率论，计算数学等分科中都有应用，也是研究具有无限个自由度的物理系统的数学工具。只有在泛函分析的框架中才有可能更深刻地理解量子力学。

自然界中最重要的过程由复杂的非线性偏微分方程所描述。其中有流体动力学、气体动力学、弹性理论、化学过程、广义相对论（宇宙学）、量子电动力学、规范场论（在基本粒子理论中的标准模型）等方面的方程。非线性项的出现相应于相互作用。

[编辑] 分支领域

泛函分析（圆形鼓皮的理想化振动模式）

...

[编辑] 数学家

[编辑] 研究所

[编辑] 著名学府数学系

[编辑] 项目

Awesome Mathematics Resources Awesome.png

Mathematics Software

[编辑] IMO

IMO

International Mathematical Olympiad (IMO)

[编辑] 菲尔兹奖

菲尔兹奖（Fields Medal） 数学界的诺贝尔奖

[编辑] 沃尔夫数学奖

沃尔夫数学奖获得者

[编辑] 阿贝尔奖

The Abel Prize 阿贝尔奖是一项挪威设立的数学界大奖

[编辑] 柯尔奖

柯尔奖（Cole Prize ，Frank Nelson Cole Prize） 由美国数学学会授奖。分数论奖和代数奖，分别奖励数论和代数领域的成果。

  • 2014 数论奖 张益唐
  • 2021 代数奖 许晨阳

[编辑] 图书期刊

[编辑] 课程

[编辑] 图集

  • 数学谱系

  • 数学的各个分支

  • 有限简单群的周期表

  • 数学家

  • 古今数学思想

  • Mathcha

  • E=mc2

  • 数学表达式

  • 数学对象

  • 基础与哲学

  • 纯粹数学-数量

  • 纯粹数学-结构

  • 纯粹数学-空间

  • 纯粹数学-变化

  • 应用数学

  • 函数与极限

  • 一些数学符号的历史

  • TeX希腊字母

  • 希腊字母表

  • 希腊字母表

  • GeoGebra

  • 箕舌线（阿涅西的女巫）

[编辑] 希腊字母

  • Mu

  • Nu

[编辑] 链接

来自“http://wiki.huihoo.com/wiki/?title=Mathematics&oldid=166936”
分享您的观点
个人工具
名字空间

变换
操作
导航
工具箱